Stochastic Particle Acceleration in Gamma-Ray Burst

A second relativistic particle component in GRB afterglow: Insights from LHAASO's observation on GRB 221009A

Abstract

Particles can be accelerated in strong turbulence by stochastic acceleration mechanism. We explore the transit-time acceleration within quasi-linear theory of turbulence and take into account the non-linear feedback to turbulence spectrum with a Fokker-Planck approach. The stochastic acceleration model predicts hard electron spectra extending to very high energies in GRB afterglow, contributing to the TeV radiation. This model is applied to the brightest gamma-ray burst GRB 221009A. By assuming that a fraction of particles in the forward shock are transported into downstream by advection and accelerated via turbulence, this model successfully explains the hard afterglow radiation spectrum at VHE band of GRB 221009A and is consistent with the multi-wavelength observations.

Background

GRB221009A is referred to as the Brightest-Of-All-Time gamma ray burst due to its intrinsic brightness (\(E_0 \sim 1.5\times 10^{51} \rm{erg}\)) and proximity ($z = 0.151$) (Burns et al. 2023). LHAASO recorded more than 64,000 Photons at $0.2-7 \rm{TeV}$ between 0-3000s after trigger with WCDA (LHAASO Collaboration 2023a), and further reported detection of 140 gamma-ray s above 3 TeV at \(230-900\)s after trigger by KM2A (LHAASO Collaboration 2023b). The recorded hard spectrum at afterglow phase cannot be explained with the one-zone SSC model. PIC simulation shows stochastic particle acceleration can produce a hard \(p\sim 1\) electron spectrum when synchrotron cooling is present (Comisso et al. 2021), potentially accounting for the hard spectrum.

Physical Picture

In the shock SSC model, upstream ISM particles being swept into the forward shock of the afterglow form a non-thermal power-law distribution due to diffusive shock acceleration. These electrons contribute to the SED in VHE band by the inverse Compoton scattering off their own synchrotron photons. It is believed that the electrons in the shock emits radiation ranging from radio to TeV gamma-ray.

Upstream rest energy could turn into turbulence in downstream. If non-thermal particles at shock front are injected into the turbulence, they will gain energy from interaction with MHD wave in either resonant or non-resonant way. This is a type-II Fermi acceleration mechanism. We explore the radiation of the electron accelerated via turbulence, which is a second radiation component in addition to the shock SSC radiation.

Skizze of the physical picture

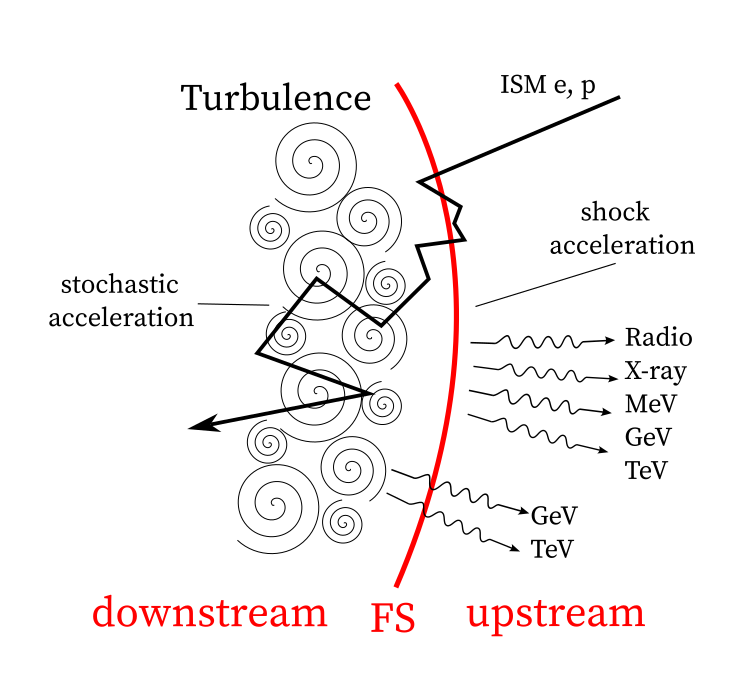
Wave Particle Interaction

According to the quasi-linear theory (QLT) of weak turbulence, particle is in resonance with turbulence when \(k_\parallel v_\parallel - \omega_F + n\Omega = 0\),with gyro-resonant interaction for \(n\neq 0\), and non-resonant transit-time damping(TTD) for \(n=0\). In the regime of strong turbulence, as the case of most astrophysical conditions, some non-linear effects are present, including resonance broadening, increasing the contribution of TTD. We only take the TTD into consideration, since we’ve found that in our case the damping could be strong, so that only turbulence around the injection scale are present. Thus only particles with highest energies are accelerated by gyro-resonance, where radiation cooling is fast and acceleration is ineffective. We adopt the phenomenological treatment of particle diffusion from (Lemoine et al. 2024),

\[D_{EE} \propto \int \Phi(E,k)W_F(k) \rm{d}k \text{,}\] \[\Phi(k,E) \propto \left\{ \exp\left[\frac{\ln (Ek/eB_0)}{\Delta_1 }\right]+ \exp\left[\frac{-\ln (Ek/eB_0)}{\Delta_2}\right]\right\}^{-1} \text{,}\]

Model Description

We describe the dynamical evolution of the GRB afterglow with Huang et al. 1999,

\[\frac{\rm{d}\Gamma}{\rm{d} m} = -\frac{\Gamma^2-1}{M_{ej} + \epsilon m + 2(1-\epsilon)\Gamma m}\label{dynevo}\text{.}\]

Similar to recent work Zhang et.al. 2021, we take a Fokker-Planck approach to model the particle diffusion in energy space and MHD turbulence cascade in wave number space,

\[\frac{\partial N}{\partial t} = \frac{\partial }{\partial E}\left[D_{\mathrm{EE}}(E,t) \frac{\partial N}{\partial E}\right] - \frac{\partial }{\partial E}\left[\left(\frac{2D_{\mathrm{EE}}(E,t)}{E} + \langle \dot{E} \rangle \right)N\right] - \frac{N}{t_{\mathrm{esc}}} + Q_{\mathrm{inj}}(E,t) \text{.}\] \[\frac{\partial W}{\partial t} = \frac{\partial }{\partial k}\left[D_{\mathrm{kk}}(k,t) \frac{\partial W}{\partial k}\right] - \frac{\partial }{\partial k}\left[\frac{2D_{\mathrm{kk}}(k,t)}{k}W\right] + \frac{k}{3}(\nabla\cdot \mathrm{v}) \frac{\partial W}{\partial k}+ \Gamma_{\mathrm{w}}(k,t) W + Q_{\mathrm{w,inj}}(k,t)\]

The two Fokker-Planck equations are coupled together by the particle diffusion term \(D_{EE}\) and the wave damping term \(\Gamma_WW(k)\).

Results

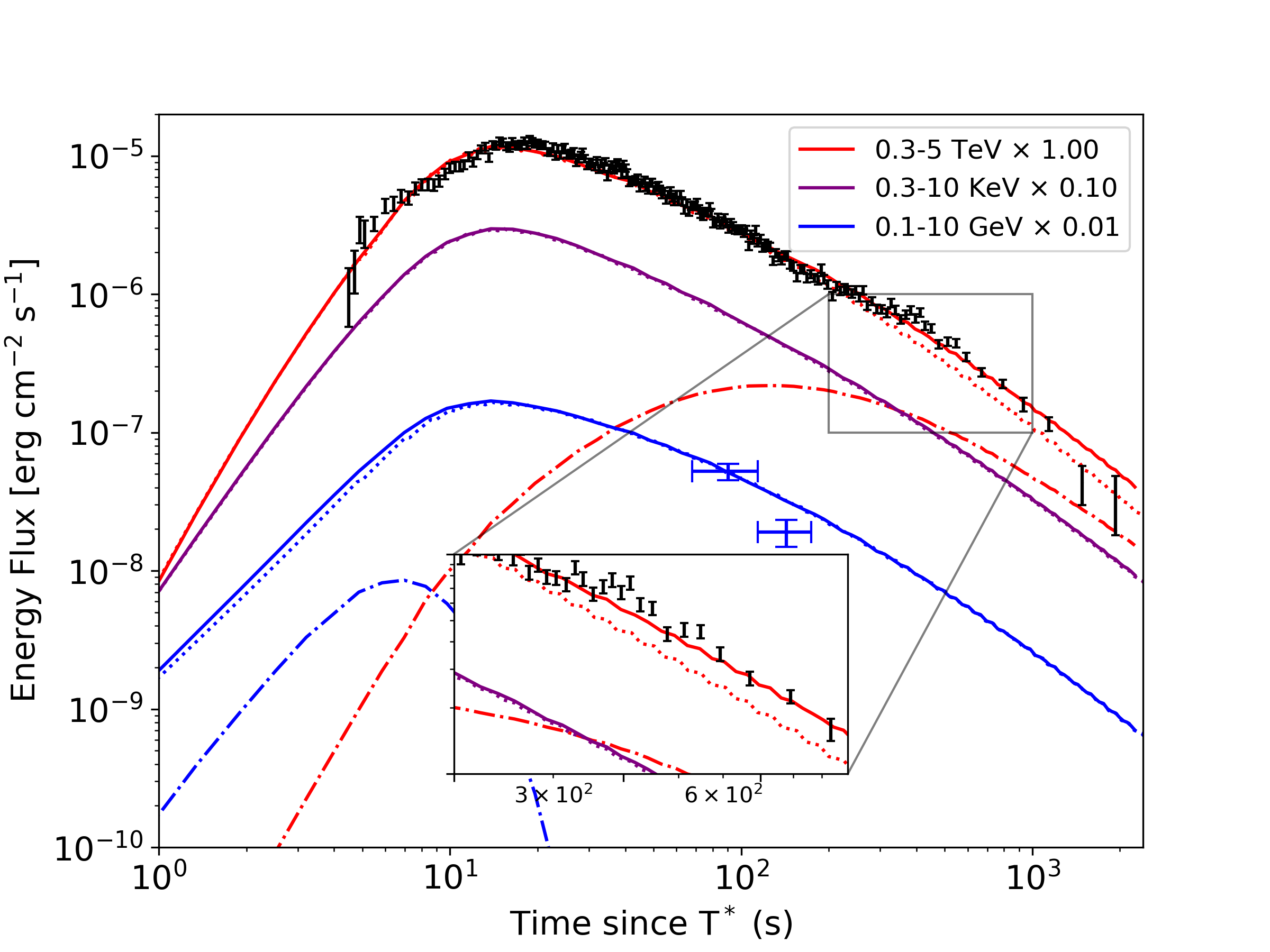
Left: Light Curve at different energy band. Solid: turbulence + shock; dash-dotted: shock only. Data points are LHAASO WCDA observation (black) and Fermi-LAT (blue) ( LHAASO Collaboration 2023b), Blue data points: Observation from Fermi LAT

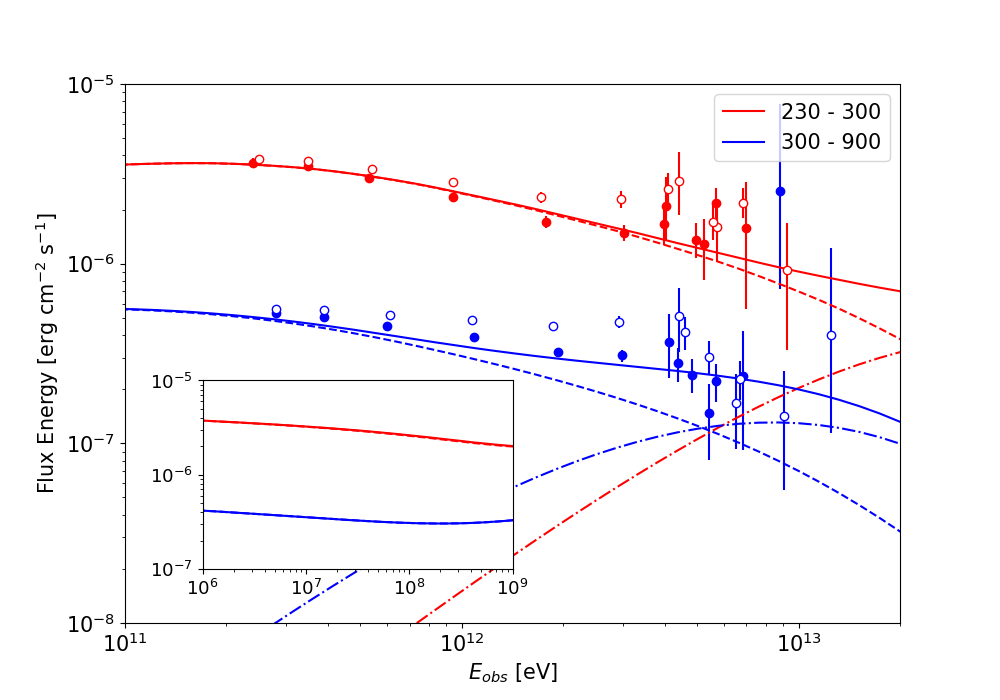
Radiation Spectra in VHE band, averaged to two time bins, same as ( LHAASO Collaboration 2023b). Data points are reduced with EBL model ( LHAASO Collaboration 2023b), filled and open circles represent the absorption-corrected flux with EBL models of Saldana-Lopez 2021 and Finke 2010 respectively ( Saldana-Lopez et al. 2021, Finke et al. 2021). SSC to first order and the intrinsic \(\gamma\gamma\) absorption are considered. Inset displays the MeV to GeV radiation, where synchrotron radiation of this component is not significant.

Spectral index evolution. Red: shock+turbulence; Blue: shock only. The hard spectrum is well explained under this model.

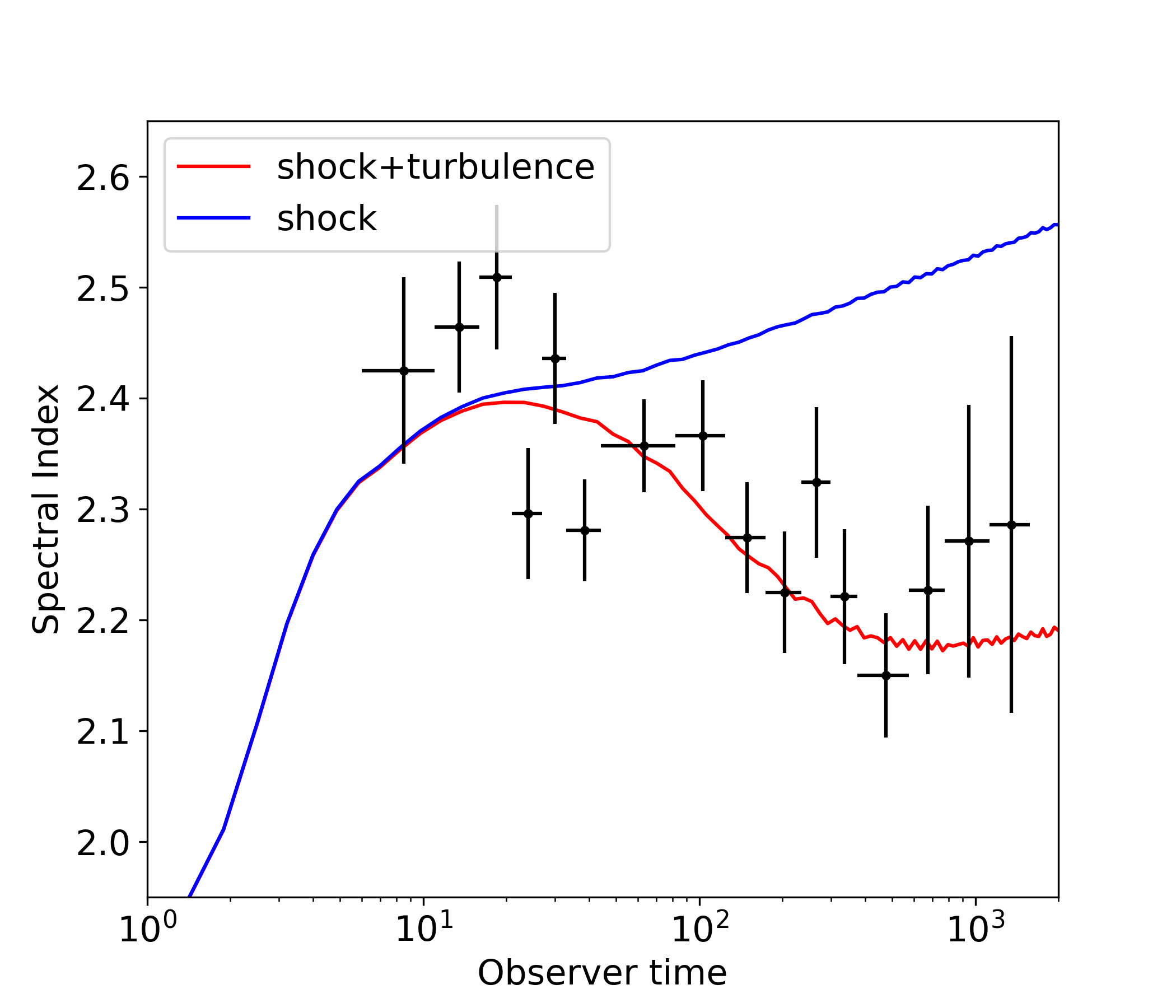
Summary

  • The SA model plays minor role at early stage, because of the strong \(\gamma\gamma\) absorption. Later it hardens the VHE spectrum after \(T^*+100\)s, leading to better agreement with the LHAASO KM2A observation.

  • Unlike Zhang et al. 2021, SA cannot accelerate proton to ultra-high energy in this event, which is mainly due to the small magnetic equipartition factor.

  • Our model cannot explain the high energy bump at \(\sim 10\)TeV due to the spectral index limit of IC. The bump may just be a result of uncertainty of EBL models.

  • Given a larger magnetic equipartition factor, the synchrotron radiation of turbulence accelerated electrons produce GeV excess before \(T^*+ 10\)s, which requires quick response of gamma-ray follow-up observations. Besides, the hard spectrum predicted by SA model can extend to above 10 TeV before \(T^*+100\)s. These features offer chances to validate our model if observations above 10 TeV for other GRBs are made in the future.

This post is from a poster presented on the 2nd LHAASO Collaboration Conference on 10/27/2024, Chengdu, China. Poster could be found under this link Poster